Problém stredovekého matematika Leonarda Fibonacciho o králikoch

Pozrime sa, ako počet králikov rastie za prvých šesť mesiacov:

1. mesiac Jeden pár mladých králikov.

2. mesiac. Stále je tu jeden pôvodný pár. Králiky ešte nedosiahli plodný vek.

3. mesiac. Dva páry: pôvodný, ktorý dosiahol plodný vek, a pár mladých králikov, ktoré porodila.

4. mesiac. Tri páry: jeden pôvodný pár + jeden pár králikov, ktoré porodila začiatkom mesiaca + jeden pár králikov, ktorí sa narodili v treťom mesiaci, ale ešte nedosiahli pohlavnú dospelosť.

5. mesiac. Päť párov: jeden pôvodný pár + jeden pár narodený v treťom mesiaci a dosiahol plodný vek + dva nové páry, ktoré porodili + jeden pár, ktorý sa narodil vo štvrtom mesiaci, ale ešte nedosiahol zrelosť.

6. mesiac. Osem párov: päť párov z minulého mesiaca + tri novonarodené páry. Atď.

Aby sme to spresnili, zapíšme si prijaté údaje do tabuľky:

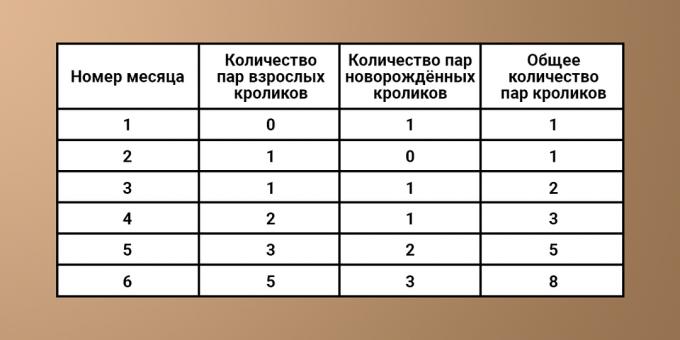
Ak tabuľku dôkladne preskúmate, môžete určiť nasledujúci vzor. Zakaždým, keď sa počet králikov prítomných v n-tom mesiaci rovná počtu králikov v (n - 1) -tom predchádzajúcom mesiaci, súčet s počtom novonarodených králikov. Ich počet sa zase rovná celkovému počtu zvierat k (n - 2) mesiacu (čo bolo pred dvoma mesiacmi). Odtiaľto môžete odvodiť

vzorec:

F_n = F_{n - 1}+ F._{n - 2},

kde F_n - celkový počet párov králikov v n-tom mesiaci, F_{n - 1} Je celkový počet párov králikov v predchádzajúcom mesiaci a F_{n - 2} - celkový počet párov králikov pred dvoma mesiacmi.

Spočítajme pomocou neho počet zvierat v nasledujúcich mesiacoch:

7. mesiac 8 + 5 = 13.

8. mesiac. 13 + 8 = 21.

9. mesiac. 21 + 13 = 34.

10. mesiac. 34 +21 = 55.

11. mesiac. 55 + 34 = 89.

12. mesiac. 89 + 55 = 144.

13. mesiac (začiatok budúceho roka). 144 + 89 = 233.

Na začiatku 13. mesiaca, teda na konci roka, budeme mať 233 párov králikov. Z toho 144 párov budú dospelí a 89 mladých. Výsledná postupnosť 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 nazývané Fibonacciho čísla. V ňom sa každé nové konečné číslo rovná súčet predchádzajúce dva.