Zahrejte pre mozog: môžete vyriešiť problém s falošnými mincami? Skontrolovať to!

Matematik má iba tri pokusy, takže nemôžete vážiť každú mincu zvlášť. Musíte ich rozdeliť na hromady a položiť na váhu po niekoľkých kúskoch, postupne sa približovať k tej falošnej.

Predpokladajme, že matematik sa rozhodol rozdeliť 12 mincí na tri kôpky, z ktorých každá má štyri mince. Potom dal na každú váhu štyri mince. Toto váženie môže poskytnúť dva výsledky. Zvážme každý z nich.

1. Váha dvoch kôp mincí bola rovnaká. Preto sú všetky peniaze v nich skutočné a falzifikát leží niekde medzi štyrmi neváženými mincami.

Na sledovanie výsledku matematik označí všetky skripty nulou. Potom z nich vezme tri a porovná ich s tromi neváženými mincami. Ak je ich váha rovnaká, potom je zvyšná (štvrtá) nevážená minca falošná. Ak je váha iná, matematik dá plus trom neoznačeným minciam, ak sú ťažšie ako mince s nulou, alebo mínus, ak sú ľahšie.

Potom si vezme dve minceoznačené plus alebo mínus a porovnáva ich hmotnosť. Ak je rovnaký, zostávajúca kópia je falošná. Ak nie, matematik sa pozrie na znamenia: medzi mincami s plusom bude falošný ten, ktorý je ťažší, medzi mincami s mínusom ten, ktorý je ľahší.

2. Váha dvoch kôp mincí nebola rovnaká.

V takom prípade musí matematik postupovať takto: označiť peniaze na ťažkej kôpke s plusom, na ľahkej kôpke s mínusom, na neváženej kôpke s nulou, pretože je známe, že falošná kópia bola na váhe.

Teraz musíte mince preskupiť, aby ste udržali hodnoty do dvoch zvyšných vážení. Jedným zo spôsobov je vziať namiesto troch mincí s plusom, troch mincí s mínusom a na ich miesto umiestniť tri kúsky s nulou.

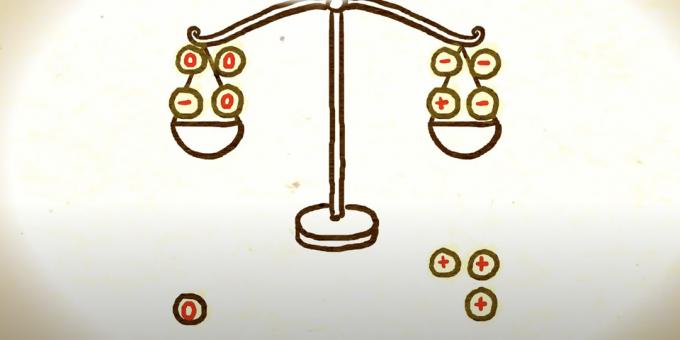
Nasledujú tri možné možnosti. Ak tá stupnica, ktorá je ťažšia, stále prevažuje, potom je buď stará minca so znamienkom plus ťažšia ako ostatné, alebo minca so znamienkom mínus na druhej strane váh. Matematik si musí vybrať ktorúkoľvek z nich a porovnať ju s bežným vzorom, aby našiel falošný.

Ak sa váha, ktorá bola ťažšia, stala ľahšou, potom je jedna z troch mincí so znamienkom mínus posunutých matematikom najľahšia. Teraz musí porovnať dve z nich na váhe. Ak sú výsledky vyrovnané, tretia minca bude falošná. V prípade nerovnosti je falošný ľahší.

Ak sú misky po výmene vyvážené, jedna z troch mincí odobratých z váh so znamienkom plus je ťažšia ako ostatné. Matematik musí porovnať dva z nich. Ak sú si rovné, tretí je falošný. V prípade nerovnosti je falošný ten, ktorý je ťažší.

Cisár súhlasne prikyvuje, keď počúva úvahy matematika, ale nepoctivý guvernér ide do väzenia.

Toto puzzle je prekladom videa TED-Ed.